Dries Buytaert

Mollom blocks more than 500,000 comment spam attempts a day. That volume provides a unique perspective on the world of comment spammers, including the world's best and worst spam techniques. Below are some excerpts from some of the more interesting spam attempts which we see frequently on Mollom's back end.

1. Some spammers try to embed flash objects in the comments section of a blog post or article. Really? Yes.

2. Spammers randomly generate spam messages as illustrated by the excerpt shown below. Some comment spammers have obviously buggy scripts ...

3. Some spammers try to take advantage of other companies' positive brand and reputation. In the example below, the spammer tries to leverage Facebook's reputation to build a positive Mollom or Akismet reputation of its own.

4. In the example below, this spammer used a free site building service, webs.com, to build a spam site. If not a free website building service, spammers will abuse incorrectly configured content management systems. Of course, there is some good old shouting too.

5. A very common spam technique is to copy relevant content from a site, and to sprinkle in some advertising. The excerpt below shows a spam message posted on a blog post that talks about Drupal.

6. As strange as it may seem, there are spammers that will simply post gibberish. My unproven theory is that they keep track of the gibberish they posted, and then register the domain after it has a reasonable ranking on Google. Spam first, create the spam pages later. This is one of the more difficult techniques to block for Mollom.

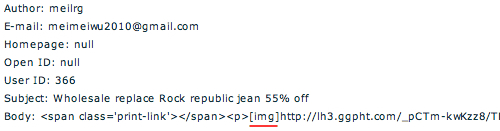
7. Then there are spammers who try to leverage image tags to inject image spam in the comments of a blog post.

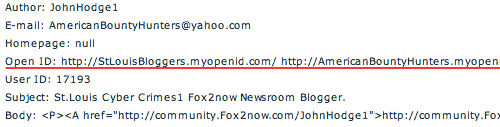
8. Some will try to use OpenID to by-pass e-mail verification.

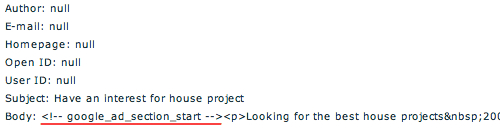
9. Another trick that spammers will try is to insert the Google ad section start. This tag is normally used by site owners to tell Google about the text and HTML content that they'd like Google to emphasize when matching ads to a site's content. Spammers try to trick Google into believing that their spam comment is the most important content on the page. Could be deadly for your search engine ranking, and could really hurt your advertising revenue. Evil!

10. Last is the simple, but somewhat clever approach of trying to trick spam filters by injecting unnecessary spacing.

There are other techniques but this should give you a sense of the strategies used by comment spammers. It seems like they are becoming more and more creative every day!